Exploration 11 - Floral Patterns in Polar Equations
First, if you are not familiar with polar equations or the polar coordinate system, I highly recommend a brief wikipedia reading to catch you up to speed: https://en.wikipedia.org/wiki/Polar_coordinate_system
Now, you might be asking, "Why would I teach polar coordinates to high school students? How is this even useful to them?" There are many contextual examples that use polar coordinates:
In essence, many physics, engineering, and biology studies (among other subjects) can have problems that are reviewed and solved by the polar coordinate system.
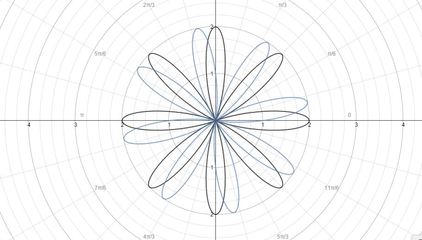
Now, let us begin with a simple exploration outlined above. I first began by exploring the cosine equation, which you can perform on my desmos tool by clicking on the image below, or by clicking here: https://www.desmos.com/calculator/au4hb8lnra
Now, you might be asking, "Why would I teach polar coordinates to high school students? How is this even useful to them?" There are many contextual examples that use polar coordinates:
- Lessons defining the Archimedean Spiral
- Studies of Circular and Orbital Motion
- Position and Navigation Studies (aircraft and ship navigational systems)
- Systems displaying radial symmetry or with a radial force (gravitational fields, groundwater flow, etc.)
- Asymmetric systems (Microphone recording studies at various frequencies, etc.)
In essence, many physics, engineering, and biology studies (among other subjects) can have problems that are reviewed and solved by the polar coordinate system.
Now, let us begin with a simple exploration outlined above. I first began by exploring the cosine equation, which you can perform on my desmos tool by clicking on the image below, or by clicking here: https://www.desmos.com/calculator/au4hb8lnra
I first began the exploration as expected, and found that when I let a=b, I found that the number of petals of the rose was equal to the integer k. In fact, k determined the number of petals I had in general. This is because in my trig functions, when I increase my |k|, I shorten the length of my period of the wave. This means I increase the number of waves within a rotation of a circle, which explains why I have more petals as I increase the absolute value of k.
I then explored the impact of the absolute value of a (|a|). When I increased this value, the petals spaced out more and became less connected. I was confused by this at first, as in the cartesian plane when I am simply looking at the cosine function, a would translate my function up or down, not change my magnitude (dilate the function). I have to remember, we are looking at a function that is comparing angle and distance, so it makes sense that if I increase my distance, I spread out the petals of a rose until they are almost not recognizable anymore.
As I increased the impact of the absolute value of b, I found that I could increase the rows of petals in my rose, or the magnitude of those petals increased (the petals were dilated). This I interpreted as a magnitude or dilation change in my standard function. While I am not an expert, it makes some sense.
It also seems that when |a|>|b| that a slight inward loop is generated inside some petals.
I also added a sine function to my polar study that you can play with. You will see that, as expected, the sine function is simply a shifted version of the cosine function, just like it is in the cartesian plane. To understand why, think about a right triangle and the unit circle.
To be honest, I would need to spend hours really understanding the behavior and patterns of these functions to give this a much better write-up. I need to explore how to better use polar equations and polar coordinates in my classroom!
See the videos below for some of my explorations!
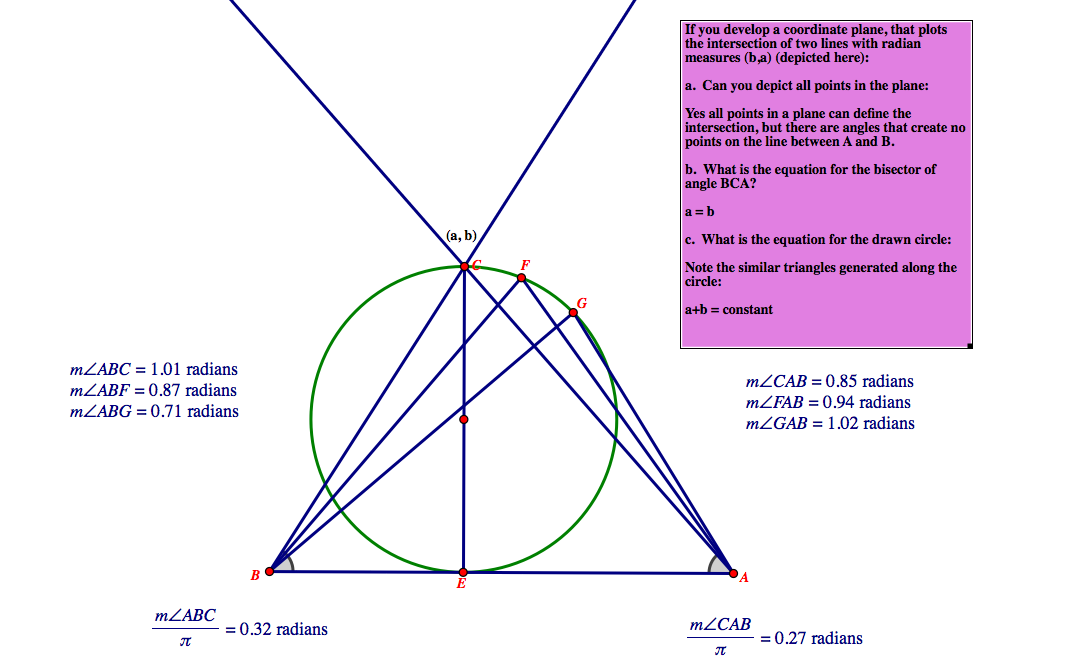
Activities that work on geometric and visual interpretation of data are useful in understanding the analysis and connection of data to students. In the task below, students are asked to work in a new plane and understand why different planes are developed and useful to study:
I then explored the impact of the absolute value of a (|a|). When I increased this value, the petals spaced out more and became less connected. I was confused by this at first, as in the cartesian plane when I am simply looking at the cosine function, a would translate my function up or down, not change my magnitude (dilate the function). I have to remember, we are looking at a function that is comparing angle and distance, so it makes sense that if I increase my distance, I spread out the petals of a rose until they are almost not recognizable anymore.
As I increased the impact of the absolute value of b, I found that I could increase the rows of petals in my rose, or the magnitude of those petals increased (the petals were dilated). This I interpreted as a magnitude or dilation change in my standard function. While I am not an expert, it makes some sense.
It also seems that when |a|>|b| that a slight inward loop is generated inside some petals.
I also added a sine function to my polar study that you can play with. You will see that, as expected, the sine function is simply a shifted version of the cosine function, just like it is in the cartesian plane. To understand why, think about a right triangle and the unit circle.
To be honest, I would need to spend hours really understanding the behavior and patterns of these functions to give this a much better write-up. I need to explore how to better use polar equations and polar coordinates in my classroom!
See the videos below for some of my explorations!
Activities that work on geometric and visual interpretation of data are useful in understanding the analysis and connection of data to students. In the task below, students are asked to work in a new plane and understand why different planes are developed and useful to study:
|
|
|