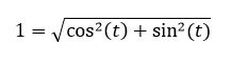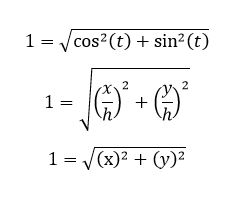Exploration 10 -
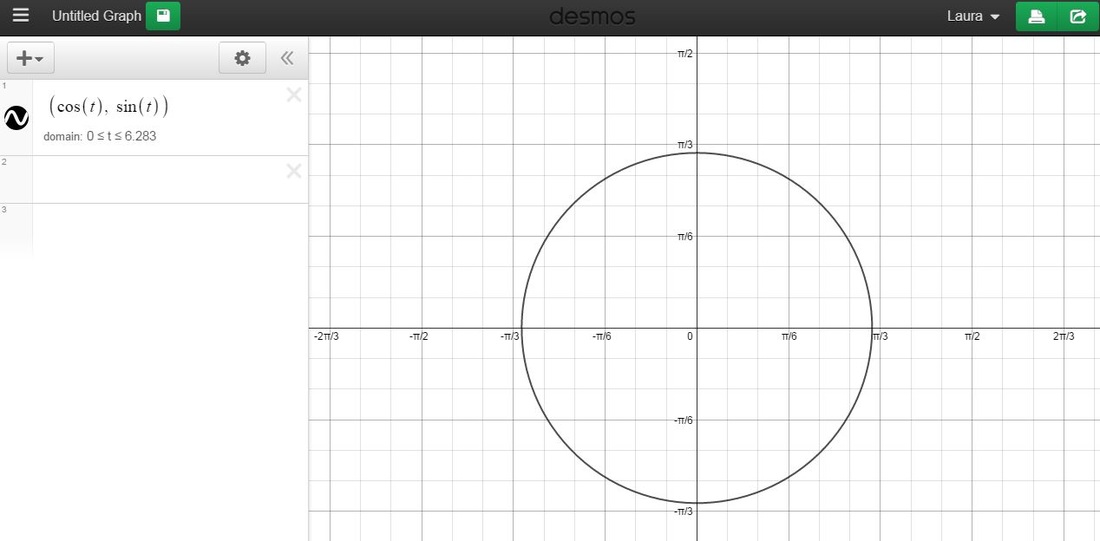
First, let's set-up our function graph in Desmos (to view yourself click on the image below or click here: https://www.desmos.com/calculator/h7iub7bvb7):
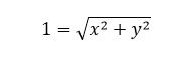
We have just generated the unit circle! Have students first write an equation for a circle with a unit radius and center at (0,0):
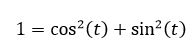
You can also use some other depictions to explain the unit circle:
Cosine function: https://www.desmos.com/calculator/s8jg20tfws
Sine function: https://www.desmos.com/calculator/kxfekf0kgb
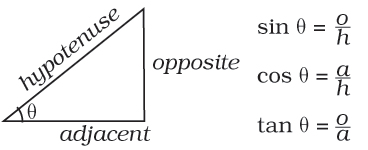
Your students should also be able to understand the following trig identity property from this depiction:
Cosine function: https://www.desmos.com/calculator/s8jg20tfws
Sine function: https://www.desmos.com/calculator/kxfekf0kgb
Your students should also be able to understand the following trig identity property from this depiction:
|
Now, let's explore some more complicated depictions:
Explore yourself here: https://www.desmos.com/calculator/8pdqk1ewkx First, let's talk about setting b = 1 and playing with a. As |a| increases, the period of the function seems to decrease in size and these increased waves in the function seem to wrap themselves around the y-axis. The entire structure, which almost appears like a bracelet seems to orbit around the x-axis as well. Next, let's talk about setting a = 1 and playing with a. As |b| increases, the period of the function seems to decrease in size and these increased waves in the function seem to wrap themselves around the x-axis. The entire structure, which almost appears like a bracelet seems to orbit around the y-axis as well.
Now, it get's interesting when we animate both a and b. When a>b, it appears that the entire structure orbits around the y-axis. When a<b, it appears that the entire structure orbits about the x-axis. The wrapping of the period changes frequently in a crossing pattern, sometimes about y=x or y=-x and sometimes just about the origin. At times the same wrap and orbit patterns seem to happen about the y = x and y = -x axis. At other times, the orbital or wrap patterns seem to almost happen about what might be the z axis if we were working in R2. It's quite fun to watch though!
|
|