Exploration 08 - Triangle Centers

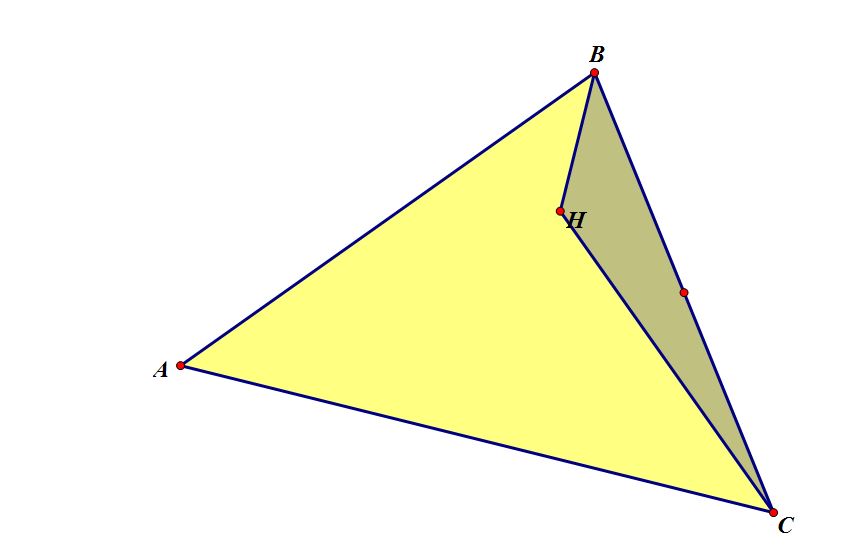
The Orthocenter of Triangle HBC is A.
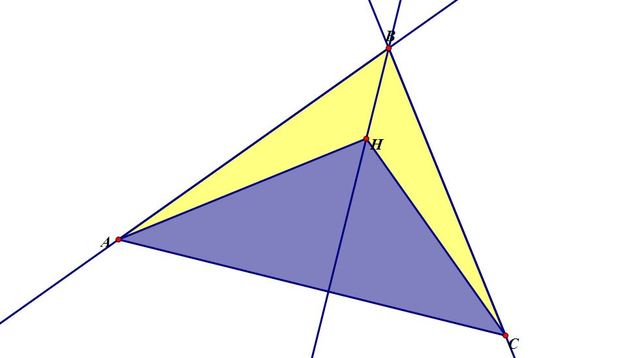
The Orthocenter of Triangle AHC is point B.
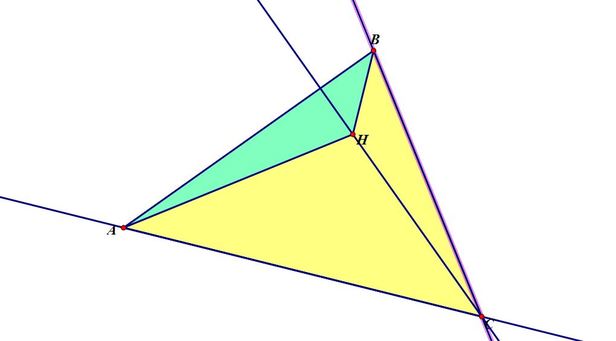
The Orthocenter of Triangle AHB is Point C.
The reason Orthocenter of the new triangle ABH is C (or any of the above results is quite simple. Think about how the Orthocenter is constructed by definition:
|
As you can see from the construction, H is constructed by the intersection of lines EC, AF, and BG which are perpendicular to AB, BC, and AC, respectively. When we form new Triangle ABH, you see that line BH is within line BG and line AH is contained within line AF.. This means that BH is perpendicular to AC and AH is perpendicular to BC. We also already knew That line AB was perpendicular to EC as well. When we find the Orthocenter again, this means we are finding lines perpendicular to AB, BH, and AH. These lines will be parallel to AF, BG, and EC respectively. Since these new parallel lines are not parallel to each other, we know that they have to meet at one and only one point, as three lines cannot intersect more than once. Since the line parallel to EC must pass through H, we know that it must pass through point C as well (as it recreates our first Ortocenter construction line). When then know that the intersection of these three lines HAS to be at point C.
|
| circle07.gsp | |
| File Size: | 12 kb |
| File Type: | gsp |