Exploration 09 - Petal Triangles
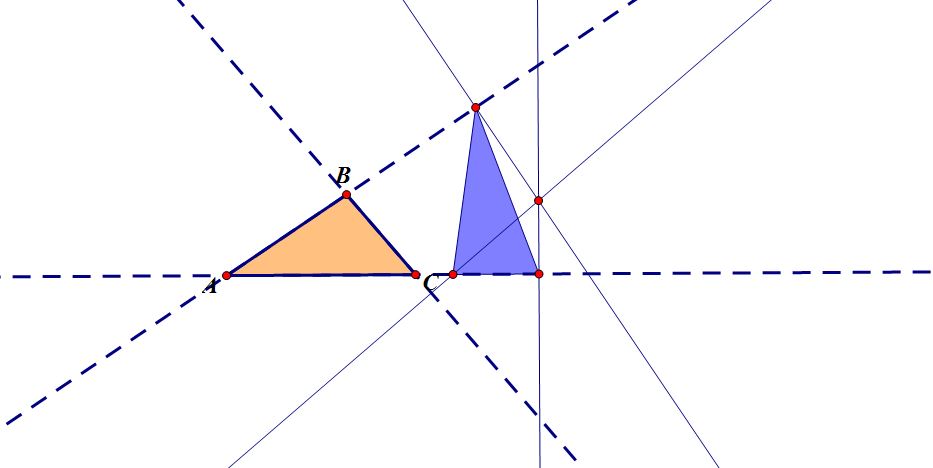
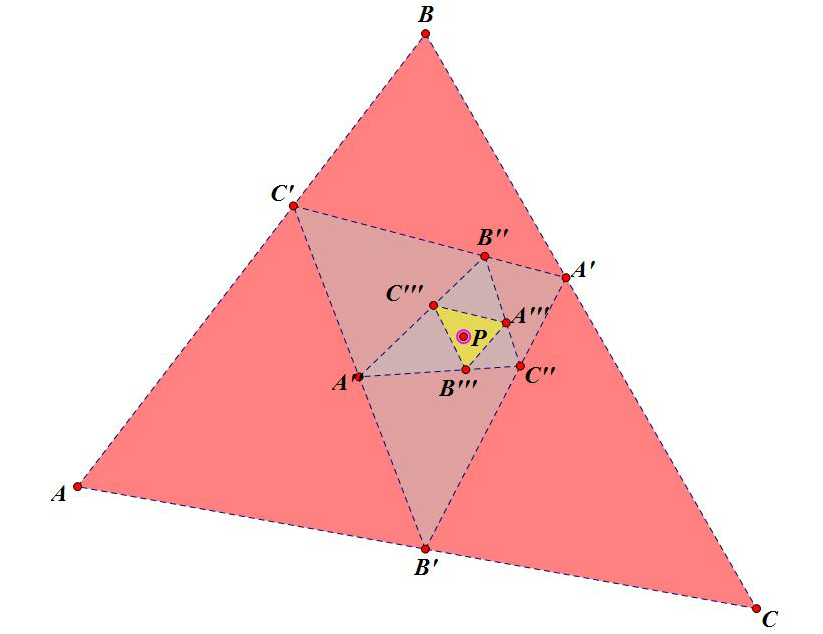
First, as you can see in Exploration 5 as well, I generated a script to create a petal triangle, you can also refer to my petal triangle exploration in the GSP file found attached below.
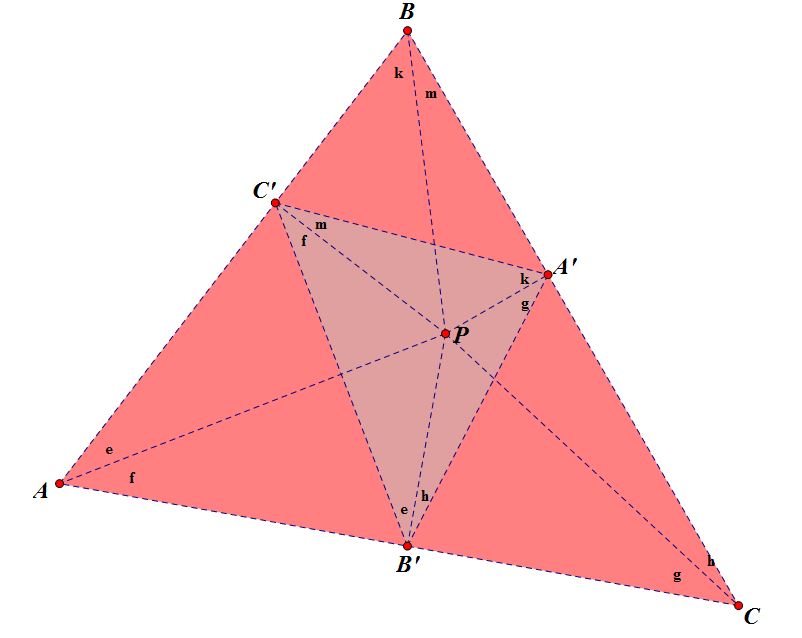
Based upon how our petal triangle was created with perpendicular lines, I can create a series of right triangles and label all congruent angles of the first two triangles above, which I will do below.
And based on our construction of right triangles via perpendicular lines in the construction of a petal triangle, I will continue labelling congruent angles.
So, the following is true based upon the diagrams above:
Angle A = e + f
Angle B = k + m
Angle C = g + h
Angle A’ = k + g
Angle B’ = e + h
Angle C’= f + m
Angle A’’= m + h
Angle B’’= f + g
Angle C’’=e + k
Angle A’’’= e + f
Angle B’’’= k + m
Angle C’’’ = g + h
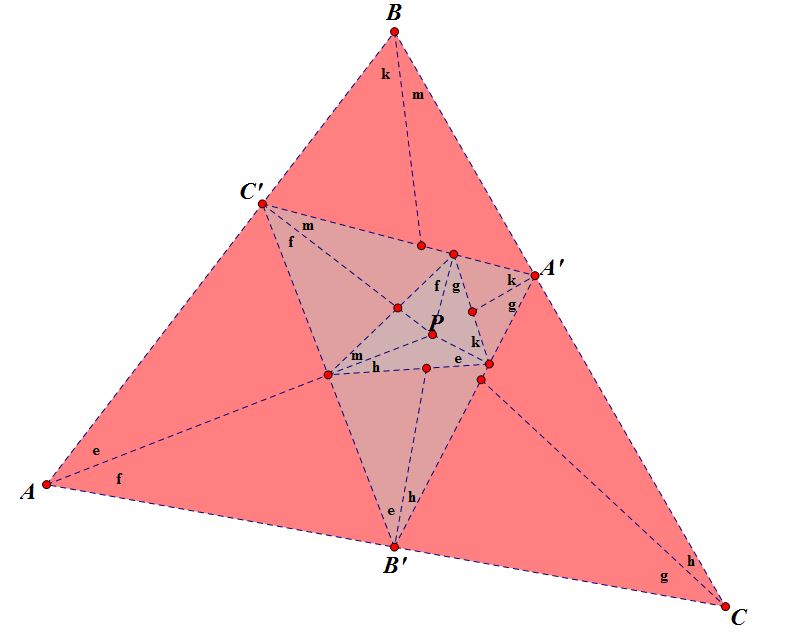
Therefore, Angle A = Angle A’’’
Angle B = Angle B’’’
Angle C = C’’’
Using AAA, I can therefore say that Triangle ABC is similar to Triangle A’’’B’’’C’’’.
Angle A = e + f
Angle B = k + m
Angle C = g + h
Angle A’ = k + g
Angle B’ = e + h
Angle C’= f + m
Angle A’’= m + h
Angle B’’= f + g
Angle C’’=e + k
Angle A’’’= e + f
Angle B’’’= k + m
Angle C’’’ = g + h
Therefore, Angle A = Angle A’’’
Angle B = Angle B’’’
Angle C = C’’’
Using AAA, I can therefore say that Triangle ABC is similar to Triangle A’’’B’’’C’’’.
| petal.gsp | |
| File Size: | 18 kb |
| File Type: | gsp |