Exploration 03 - Cubic Root Patterns
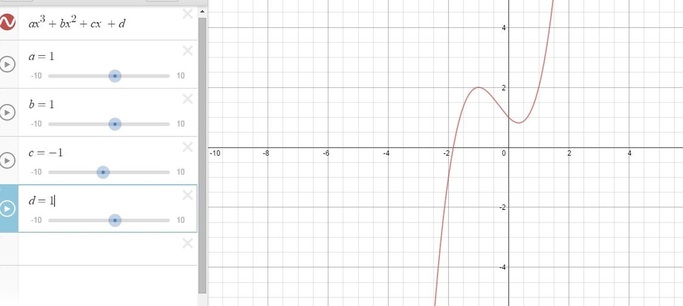
For my write-up, I'm going to discuss my exploration of this cubic function in the xd plane. To do so, I'm simply going to create a desmos slider tool and play with keeping my a, b, and c coefficients at + or - 1 and see what happens as I change my d coefficient. So, I am slightly playing in the xd field to understand root patterns here.
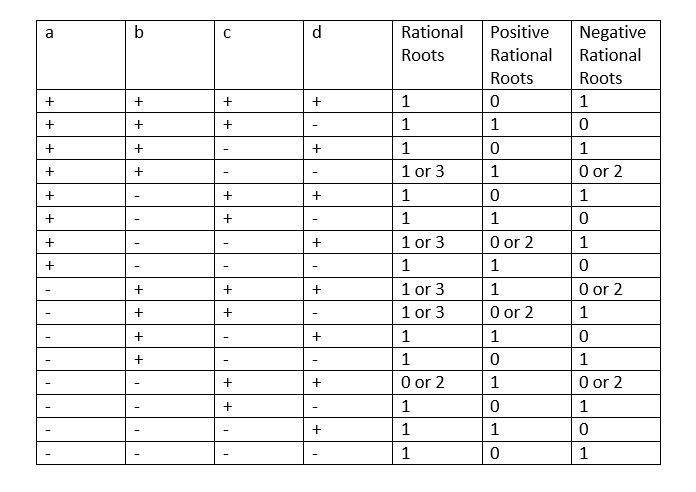
So, now I will discuss the patterns I found (Note: I am counting multiplicities as 2 roots):
So, now I will discuss the patterns I found (Note: I am counting multiplicities as 2 roots):
Now, it is easy to note that the cubic function with leading that contains leading coefficients equal to 1 or -1 for a, b, and c will always have 1 or 3 rational roots. One can also see the pattern created by translating the function up and down using d for translation that the function can only have 1 positive root or 0/2 positive roots based on it's position. The same works for negative roots. So, students might put together that this function can have 1 (mod 2) roots or 0(mod 2) roots, or simply attempt to label them as even or odd.
And if you don't know where I'm going with this. I am curious if giving students this exploration will allow them to come up with Descartes' Rule of Signs on their own, and be able to apply it to other polynomials to determine the potential number of positive and negative rational roots for a polynomial:
Descartes' Rule of Signs:
The rule states that the possible number of the positive roots of a polynomial is equal to the number of sign changes in the coefficients of the terms or less than the sign changes by a multiple of 2.
The corollary rule states that the possible number of the negative roots of the original polynomial is equal to the number of sign changes (in the coefficients of the terms after negating the odd-power terms) or less than the sign changes by a multiple of 2. (Taken from: http://hotmath.com/hotmath_help/topics/descartes-rule-of-signs.html)
Do the exploration yourself by clicking on the image below!
And if you don't know where I'm going with this. I am curious if giving students this exploration will allow them to come up with Descartes' Rule of Signs on their own, and be able to apply it to other polynomials to determine the potential number of positive and negative rational roots for a polynomial:
Descartes' Rule of Signs:
The rule states that the possible number of the positive roots of a polynomial is equal to the number of sign changes in the coefficients of the terms or less than the sign changes by a multiple of 2.
The corollary rule states that the possible number of the negative roots of the original polynomial is equal to the number of sign changes (in the coefficients of the terms after negating the odd-power terms) or less than the sign changes by a multiple of 2. (Taken from: http://hotmath.com/hotmath_help/topics/descartes-rule-of-signs.html)
Do the exploration yourself by clicking on the image below!