Final Problem - Bouncin' Barney
First, to demonstrate that Barney will always return to his starting point, I have created a GSP file and animation of all possible travels. Feel free to play around with the shape of the triangle and animation to ensure this happens!
|
|
| ||||||
When Barney starts on segment BC, he bounces on 5 walls before getting home, unless he starts at the midpoint of the segment. In that case, Barney only gets bounced 3 times.
Now, in a practical sense, if Barney is outside of the segment and goes on his parallel path, he's never actually going to ever run into a wall. For the sake of pretending the wall extends forever, Barney still returns home and encounters 5 bounds to get there.
|
| ||||||
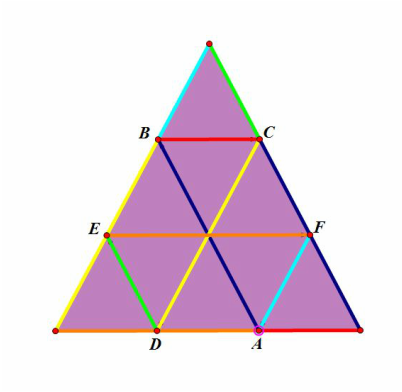
If Barney starts on the line segment he travels the same distance, if he is outside the line segment, he does not.
It's pretty easy to see that when Barney starts on the line segment inside the triangle, that he always travels the perimeter of the triangle. Because of the parallel lines and similar triangles, you can see by the color segments above that Barney is always travelling the distance of the perimeter!
There is always a pattern in which 6 congruent triangles are generated within the triangle. You can also easily have students find similar triangles to the overall triangle easily from the above image using AAA. When students see a triangle, all they need to do is match the colors of each side. As long as all three colors of the internal triangles they see are represented with colors on all three walls of the outer triangle, we can prove similarity by parallel lines. Students show find that ALL triangles are similar by the nature of the way Barney is travelling. He is travelling at only angles congruent to the angles of the triangle!